Linear Difference Equations and Asset Pricing
Honours Intermediate Macro
Solutions (and Uniqueness) of Difference Equations
From the previous lecture notes, pricing a sequence \(\left\{{y_{t+j}}\right\}\) of payoffs:
\[ P_t = \sum_{j=0}^{\infty} \beta^j y_{t+j} \quad \text{at time } t \text{ (Sequential formulation)} \]
Can be written:
\[ P_t = y_t + \beta P_{t+1} \]
Solving with Guess and Verify
How can we solve a difference equation?
Example: \(y_t=\bar{y}\)
\[ P_t = \bar{y} + \beta P_{t+1} \tag{1}\]
A Guess: \(P_t=\bar{P}\), independent of \(t\). Plug in Equation 1:
\[ \bar{P} = \bar{y} + \beta \bar{P} \quad \Rightarrow \quad \bar{P} = \frac{\bar{y}}{1-\beta}, \text{ consistent with } P=\sum_{t=0}^{\infty} \beta^t y_t \]
Role of \(|\beta|<1\):
- Keep from “exploding”: stability
- Will have equivalent condition for more complicated difference equations
Rational Bubbles
Let \(y_t=\bar{y}\) for all \(t\).
Fundamental value:
\[ P_t = \sum_{j=0}^{\infty} \beta^j \bar{y} = \frac{\bar{y}}{1-\beta} \quad \text{(unique)} \]
Remember that this solves the recursive problem as well:
\[ \frac{\bar{y}}{1-\beta} = \bar{y} + \beta \left(\frac{\bar{y}}{1-\beta}\right) \Rightarrow \text{true!} \]
Is \(P_t = \dfrac{\bar{y}}{1-\beta}\) the unique solution to \(P_t = \bar{y} +\beta P_{t+1}\)? No! Like the undetermined coefficient in differential equations.
Example:
\[ P_t = \underbrace{\dfrac{\bar{y}}{1-\beta}}_{\text{fundamental value}} + \underbrace{c \beta^{-t}}_{\text{bubble term}} \quad \text{for any } c \]
Check: \(P_t = \bar{y} + \beta P_{t+1}\)
\[ \frac{\bar{y}}{1-\beta} + c\beta^{-t} = \bar{y} + \beta \left[ \frac{\bar{y}}{1-\beta} + c \beta^{-(t+1)} \right] = \bar{y} + \left(\frac{\beta}{1-\beta}\right)\bar{y} + c\beta^{-t} = \frac{\bar{y}}{1-\beta} + c\beta^{-t} \]
So it fulfills the difference equation for any \(c,t\), etc. Rational as every agent in the economy would agree on the price, no one needs to be tricked or making a pricing mistake, and there is no arbitrage. An example of a self-fulfilling equilibrium.
Size of the “Rational Bubble”
\[ \underbrace{P_0 - P_{fund}}_{\text{difference from fundamental}} = \frac{\bar{y}}{1-\beta} - \frac{\bar{y}}{1-\beta} + c \beta^0 = c \]
Expectations:
- Prices rise because they are expected to rise.
- Self-fulfilling. Will depend on coordination of expectations.
- Is Fiat money a bubble?
Extending our Asset Pricing Model
We will generalize our results to include systems of equations, with dynamics.
Recall: Properties
- Dividend stream \(y_t\)
- Discount factor \(\beta\)
- Present discounted value = price: \(P = \sum_{t=0}^{\infty} \beta^t y_t\), and if \(y_t = \bar{y}\), \(P=\bar{y}(1-\beta)^{-1}\)
- How to model the evolution of \(y_t\)?
- Will use systems of linear difference equations in an underlying state \(x_t\)
- Example: dividends are a linear function of evolving aggregate and idiosyncratic variables
Recall: Recursive Formulation: \(P_t = y_t + \beta P_{t+1}\)
Applying to Dynamics
- Let \(x_t\) be an \(n\)-dimensional vector of states.
- Let \(A, G\) be matrices.
- Stack first order difference equations, giving another canonical form:
\[ \begin{aligned} x_{t+1} &= A \cdot x_t & \text{($A$ is $n \times n$ matrix, $x_t$ is $n \times 1$ vector)}\\ y_t &= G \cdot x_t & \text{($G$ is $1 \times n$ vector, $y_t$ is a scalar, i.e. $1 \times 1$)} \end{aligned} \]
- “\(A\)” gives evolution of the state, given \(x_0\)
- “\(G\)” gives observation of the state
- “Finding the state is an art”
Example:
- Asset payoff follows difference equation (not first order!):
\[ y_{t+1} = \rho_1 y_t + \rho_2 y_{t-1} \]
- What is the value of this asset at time \(t\)?
State:
Guess: \(x_t \equiv \begin{bmatrix} y_t \\ y_{t-1} \end{bmatrix}\), a \(2 \times 1\) vector.
What is the difference equation for \(x_t\)?
\[ \underbrace{\begin{bmatrix} y_{t+1} \\ y_t \end{bmatrix}}_{x_{t+1}} = \underbrace{\begin{bmatrix} \rho_1 & \rho_2 \\ 1 & 0 \end{bmatrix}}_{A} \underbrace{\begin{bmatrix} y_{t} \\ y_{t-1} \end{bmatrix}}_{x_t} \]
And observation:
\[ y_t = \underbrace{\begin{bmatrix} 1 & 0 \end{bmatrix}}_{G} \underbrace{\begin{bmatrix} y_t \\ y_{t-1} \end{bmatrix}}_{x_t} \]
Therefore, the set of difference equations in our canonical form are:
\[ \begin{aligned} x_{t+1} &= Ax_t\\ y_t &= Gx_t \end{aligned} \]
Price is:
\[ P_t = \sum_{j=0}^{\infty} \beta^j y_{t+j} = \sum_{j=0}^{\infty} \beta^j G \cdot x_{t+j} \]
If \(x_{t+1} = A\cdot x_t\), then \(x_{t+2} = A \cdot (A x_t) = A^2 x_t\), and \(x_{t+j} = A^j x_t\)
\[ \Rightarrow P_t = \sum_{j=0}^{\infty} \beta^j G \cdot A^j \cdot x_t = G \cdot \left[ \sum_{j=0}^{\infty} \left(\beta A\right)^j \right] x_t \]
Remember that if \(\lambda\) is scalar: \(\sum_{j=0}^{\infty} \left(\beta \lambda\right)^j = \left(1-\beta\lambda\right)^{-1} = \frac{1}{1-\beta \lambda}\).
With matrices and inverses, this is similar: \(\sum_{j=0}^{\infty} \beta^j A^j = \left(I - \beta A\right)^{-1}\),
where the matrices’ dimensions are: \(A : n \times n\), \(I = n \times n\) identity, \((I-\beta A)^{-1} : n \times n\)
\[ \boxed{P_t = G \left(I-\beta A\right)^{-1} x_t} \quad (\text{very important, memorize!}) \]
- Asset pricing formula for first-order linear difference equations.
- Summary of sizes:
- \(P_t\): \(1 \times 1\) scalar
- \(G\): \(1 \times n\) vector
- \(A\): \(n \times n\) matrix
- \(I\): \(n \times n\) identity matrix
- \(\beta\): \(1 \times 1\) scalar
- \(x_t\): \(n \times 1\) state vector
Stability
- Recall in the example with \(x_t = \lambda^t\) that \(|\beta \lambda| < 1\) for the series to converge.
- For matrix equations, need a similar condition where eigenvalues of \(\beta A\) are all \(<1\), or \(\max | \text{eig}(A) | < \frac{1}{\beta}\)
- Can use software to check the eigenvalues.
Appendices
Connection to Differential Equations
Difference equations are just differential equations in discrete time.
- Let \(y(t)\) be the flow dividends, a function of \(t\).
- Let \(r\) be the instantaneous interest rate.
- Let the length of a period be \(\Delta\), and take the limit as it goes to 0.
- Dividends over \(\Delta\) period \(\approx \Delta y(t) \equiv y_t(\Delta)\)
- Discounting over \(\Delta\) period \(\approx 1- \Delta r \equiv \beta(\Delta)\)
The difference equation is: \(P_t = y_t + \beta P_{t+1}\).
Using the above: Let function \(p(t)\) be the price of asset:
\[ p(t) = \Delta \cdot y(t) + (1-\Delta r) \cdot p(t+\Delta) \]
Rearrange:
\[ \Delta r \cdot p(t+\Delta) = \Delta \cdot y(t) + p(t+\Delta) - p(t) \]
\[ \Rightarrow r p(t+\Delta) = y(t) + \frac{p(t+\Delta) - p(t)}{\Delta} \]
Take limit as \(\Delta \rightarrow 0\), i.e. discrete \(\rightarrow\) continuous \(t\)
\[ {\boldsymbol{\partial}_{}}p(t) = \frac{p(t+\Delta) - p(t)}{\Delta} \quad \text{(definition of a derivative)} \]
where \({\boldsymbol{\partial}_{}}p(t) = \dfrac{d}{dt}p(t)\)
\[ \Rightarrow \underbrace{r p(t)}_{\text{opportunity cost of buying a unit of the asset}} = \underbrace{y(t)}_{\text{flow dividends}} + \underbrace{{\boldsymbol{\partial}_{}}p(t)}_{\text{capital gains}} \]
- Consider this pricing equation and arbitrage:
- What if \(r p(t) < y(t) + {\boldsymbol{\partial}_{}}p(t)\) instead of being an equation?
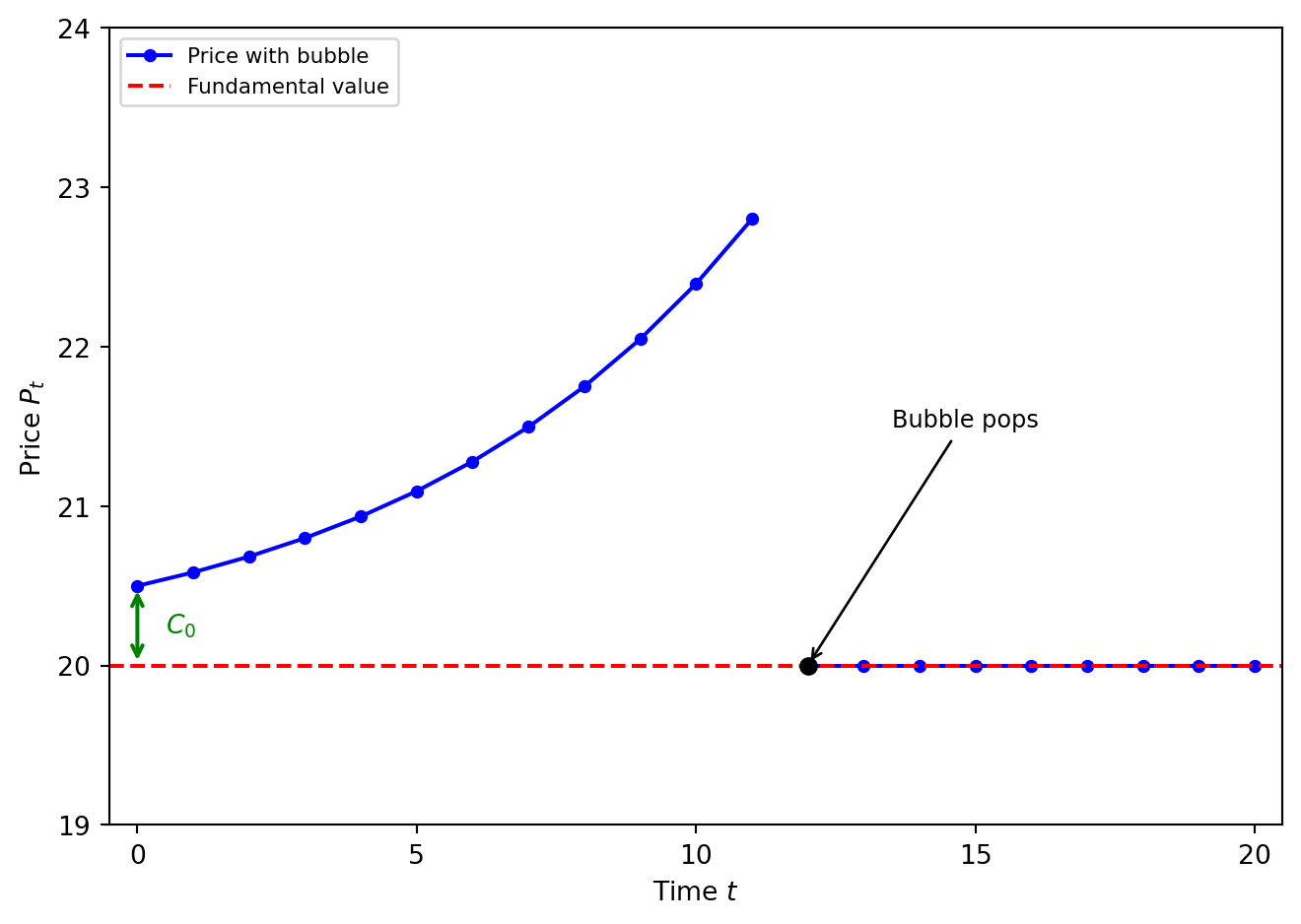
Popping Bubbles
In our discrete time model, keep \(y_t=\bar{y}\) deterministic for simplicity:
- Let the bubble term have a chance of popping each period.
- Therefore, prices are a random variable.
- Linear asset pricing if random:
\[ P_t = y_t + \beta {\mathbb{E}_{{t}}\left[ {P_{t+1}} \right]} \quad \text{(Expected value of $P_{t+1}$ given information at $t$)} \]
Bubble Evolution
\[ \text{Let } C_{t+1} = \begin{cases} \frac{1}{\lambda} C_t & \text{with prob. } \lambda \in (0,1) \\ 0 & \text{with prob. } 1-\lambda \end{cases} \]
i.e., \(C_t\) multiplied by \(\frac{1}{\lambda}\) each time until bubble breaks. Then \(C_t = 0\) for all \(t\).
Note:
\[ {\mathbb{E}_{{t}}\left[ {C_{t+1}} \right]} = \lambda \left(\frac{1}{\lambda} C_t\right) + (1-\lambda)\cdot 0 = C_t \]
If \({\mathbb{E}_{{t}}\left[ {y_{t+1}} \right]}=y_t\), then this term is called a martingale.
Price Level
We can check that for any \(C_0\):
\[ P_{t} = \begin{cases} \frac{\bar{y}}{1-\beta} + \left(\beta \lambda\right)^{-t}\cdot C_0 & \text{if bubble hasn't popped} \\ \frac{\bar{y}}{1-\beta} & \text{after bubble pops} \end{cases} \]