Natural Language Processing and Large Language Models

Graduate Quantitative Economics and Datascience

Jesse Perla
jesse.perla@ubc.ca

University of British Columbia

Overview

Summary

  • Discuss text, NLP, and other embeddings
  • Relate embeddings to transformations like PCA
  • Use LLMs via the LangChain package

References

API Options for LLMs

  • There are many ways to access these tools, including vendor-specific APIs and those which wrap things in as much of a cross-vendor way as possible
  • A big variation is between LLMs that are hosted and ones that run locally.
  • Local use of LLM/NLP is often facilitated by the package Hugging Face Transformers
    • We will not use this approach here because it requires far more background, but if you are serious this is useful to know about
  • Remote use of LLMs can be done with
    • Vendor specific APIs: e.g., OpenAI
    • Cross-vendor packages: e.g., LangChain which calls out to OpenAI/Gemini/etc.

Packages

  • For this introduction, we will use LangChain to call out to OpenAI
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import numpy as np
import tiktoken
from langchain_openai import ChatOpenAI, OpenAIEmbeddings
from langchain_core.messages import SystemMessage, HumanMessage, AIMessage

OpenAI via LangChain

  • Sign up for the OpenAI Platform
    • Sometimes it is free for a limited number of tokens. See pricing for more
  • Go to the API keys tab and create a key
  • In your terminal, set OPENAI_API_KEY to this value (see here)

Creating the LangChain API

  • Instantiate models once (LangChain will pick up OPENAI_API_KEY from environment variable)
  • The model= might be chosen for speed, cost, etc.
  • Temperature is how random to make the output (0 = deterministic). Will discuss more later.
openai_embedding_model = "text-embedding-3-large"
openai_chat_model = "gpt-4o-mini"
llm = ChatOpenAI(model=openai_chat_model, temperature=0.7)
embedder = OpenAIEmbeddings(model=openai_embedding_model)

Tokens, Vocabulary, and Corpus

Tokens and Vocabulary

  • We can define a vocabulary of \(K\) possible “tokens” enumerated \(k = 1, \ldots, K\)
    • For NLP, this might be common words, parts of words, and characters.
    • The vocabulary is model and sometimes application specific
  • A splitter will take an input and break it into pieces
    • e.g., take a sentence and split on the whitespace
  • A tokenizer will take an input and map it into a sequence of token indices
    • e.g., take a sentence, split on the spaces, and then map to tokens in the vocabulary
  • The corpus is the set of text/etc. you use
    • In specialized cases you might want to build a custom vocabulary based on how common certain words are in your corpus

Example with OpenAI Tokens

  • When using LLMs this sometimes happens in the background, but other times you may need more manual control
  • We can use a package to reverse-engineer what OpenAI does under the hood.
    • Splits on whitespace, tokens may be whole words, subwords, or characters
enc = tiktoken.encoding_for_model(openai_embedding_model)
print(f"Tokens in vocabulary for {openai_embedding_model}: {enc.n_vocab}")
print(f"'Hello world' -> {enc.encode('Hello world')}")
print(f"'hello world' -> {enc.encode('hello world')}")
print(f"'hello world 67' -> {enc.encode('hello world 67')}")
Tokens in vocabulary for text-embedding-3-large: 100277
'Hello world' -> [9906, 1917]
'hello world' -> [15339, 1917]
'hello world 67' -> [15339, 1917, 220, 3080]

Tasks with Tokens

  • Most tasks in NLP involve working with these tokenized inputs. For example,
    • Simple counts of tokens (e.g., bag of words) for comparison
    • Using a sequence of tokens as input to a model to predict the next token (or missing tokens)
    • Mapping a sequence of tokens into an embedding of the entire sequence for similarity/classification/etc.
  • Not specific to text though. Can use with any sequence of discrete or discretized outcomes

Embedding a Token

  • The ordering of the tokens from \(k = 1, \ldots, K\) is arbitrary
  • However, we can assign a real-valued vector to each token
    • This is called an embedding of the token and could capture things like conceptual similarity between them, etc.
    • The real-valued vectors can then be clustered, classified, etc.

Embeddings

What is an Embedding?

resp = llm.invoke([
    SystemMessage(content="You provide 2 short bullet points, technical answers."),
    HumanMessage(content="What is an embedding?")
])
resp_text = resp.content
print(resp_text)
- An embedding is a mathematical representation of items (such as words, sentences, or images) in a continuous vector space, where similar items are mapped to nearby points in that space.
- Embeddings are commonly used in machine learning and natural language processing to capture semantic meaning and relationships, enabling algorithms to process and analyze complex data more effectively.

Detour into OpenAI (via LangChain)

  • Our code uses LangChain message objects to call OpenAI under the hood.
  • Message roles in LangChain and their OpenAI mapping:
    • SystemMessage → OpenAI “system” role (sets behavior/instructions)
    • HumanMessage → OpenAI “user” role (your prompt/query)
    • AIMessage → OpenAI “assistant” role (model responses)
  • When building a conversation, you pass the entire message history (system + user + assistant) to the model each time; the model conditions on this full context.

LLMs are Stateless

  • When you call llm.invoke([...]) and related APIs you pass the entire history of the conversation each time.
  • This lets the model condition on the entire history to have history-contingent answers, and means it does not keep around a “state” or “memory” of the conversation.

Followup: What does it have to do with Latent Spaces?

resp = llm.invoke([
    SystemMessage(content="You provide 2 short bullet points, technical answers."),
    HumanMessage(content="What is an embedding?"),
    AIMessage(content=resp_text),
    HumanMessage(content="What is the relationship to latent spaces?")
])
print(resp.content)
- Latent spaces are abstract, lower-dimensional representations of data that capture essential features, often used in models like autoencoders and generative adversarial networks (GANs), where embeddings can serve as points within this latent space.
- Both embeddings and latent spaces aim to reduce dimensionality while preserving important information and relationships, allowing for effective data representation and manipulation in machine learning tasks.

Embeddings Overview

  • Used loosely and inconsistently, but the spirit is the same
  • A mapping of some \(x \in \mathcal{X}\) to a latent space \(\phi(x) \in \mathcal{Z}\)
  • Typically we want that \(\mathcal{Z}\) is a continuous vector space of finite dimension
    • Crucially, we can think of distances in that space (e.g., \(||\phi(x) - \phi(y)||\))
  • The dimension of \(\mathcal{Z}\) may be smaller or larger than \(\mathcal{X}\)
    • If larger, typically in only small regions of the higher-dimensional space.
  • Often want to preserve norms in cases where the original space itself had a norm
    • e.g., if \(||x - y||\) is small, then \(||\phi(x) - \phi(y)||\) is small

Cosine Similarity

  • Cosine similarity is the “angle” between two vectors in the embedding space \(z = \phi(x)\) and \(z' = \phi(x')\) \[ \mathrm{sim}(z, z') = \frac{z \cdot z'}{||z|| ||z'||} \]

Interpretation of Cosine Similarity

  • Interpretation: If \(z\) and \(z'\) are
    1. close in the embedding space, then the cosine similarity is close to 1
    2. orthogonal, then the cosine similarity is 0
    3. opposite, then the cosine similarity is -1
  • Norm comparison \(||z - z'||\) instead? Works but not invariant to scaling

Implementation of Cosine Similarity

def cos_sim(a, b):
  denom = np.linalg.norm(a) * np.linalg.norm(b)
  return np.dot(a, b) / denom
print(f"cos_sim([1, 0], [0, 1]) = {cos_sim(np.array([1, 0]), np.array([0, 1]))}")
print(f"cos_sim([1, 0], [0, 2]) = {cos_sim(np.array([1, 0]), np.array([0, 2]))}")
print(f"cos_sim([1, 0], [1, 0]) = {cos_sim(np.array([1, 0]), np.array([1, 0]))}")
print(f"cos_sim([1, 0], [2, 0]) = {cos_sim(np.array([1, 0]), np.array([2, 0]))}")
print(f"cos_sim([1, 0], [-2, 0]) = {cos_sim(np.array([1, 0]), np.array([-2, 0]))}")
cos_sim([1, 0], [0, 1]) = 0.0
cos_sim([1, 0], [0, 2]) = 0.0
cos_sim([1, 0], [1, 0]) = 1.0
cos_sim([1, 0], [2, 0]) = 1.0
cos_sim([1, 0], [-2, 0]) = -1.0

Using LangChain OpenAI Embeddings

embed_bank = embedder.embed_query("bank")
embed_banks = embedder.embed_query("banks")
embed_river = embedder.embed_query("river")
embed_money = embedder.embed_query("money")
print(f"sim(bank, banks) = {cos_sim(embed_bank, embed_banks):.4f}")
print(f"sim(bank, river) = {cos_sim(embed_bank, embed_river):.4f}")
print(f"sim(bank, money) = {cos_sim(embed_bank, embed_money):.4f}")
print(f"sim(river, money) = {cos_sim(embed_river, embed_money):.4f}")
sim(bank, banks) = 0.7882
sim(bank, river) = 0.4143
sim(bank, money) = 0.4347
sim(river, money) = 0.3747

Where Did the Embedding Come From?

  • OpenAI’s text embeddings (e.g., text-embedding-3-large) are trained with self-supervised objectives to produce general-purpose semantic vectors.
  • Conceptually, a representation map \(\phi(x)\) is learned so that cosine similarity reflects semantic relatedness.
  • Always check provider docs for the training objective and intended use; not all embeddings are suitable for every task.

Bigger Embeddings

Bag of Words

  • Words usually occur in sentences, paragraphs, etc.
  • Instead of embedding a single word, we can embed a block of text.
  • Simple starting point: compare the relative frequency of words
    1. Turn the text into blocks of tokens with unique identifiers
    2. Filter out tokens that are not useful (e.g., “the”, “a”, etc.)
    3. Count the frequency of each token
    4. The embedding is the vector of the frequency of each token
  • Many issues with this, but crucially it does not capture any sense of context dependent meaning of words, and is invariant to word order

Sentence Embeddings with LLMs

  • Encode an entire sentence into a single embedding and compare for similarity
e_1 = embedder.embed_query("The man bites the dog")
e_2 = embedder.embed_query("The dog chased the man")
e_3 = embedder.embed_query("The man was chased by the dog")
print(f"sim(e_1, e_2) = {cos_sim(e_1, e_2):.4f}")
print(f"sim(e_1, e_3) = {cos_sim(e_1, e_3):.4f}")
print(f"sim(e_2, e_3) = {cos_sim(e_2, e_3):.4f}")
sim(e_1, e_2) = 0.5414
sim(e_1, e_3) = 0.5226
sim(e_2, e_3) = 0.7911
  • Note that the 2nd and 3rd are the most similar, and the 1st and 3rd the least.

Be Cautious, Interpretation is Tricky

e_1 = embedder.embed_query("The man bites the dog")
e_2 = embedder.embed_query("The dog chased the man")
e_3 = embedder.embed_query("The man was chased by the dog")
e_4 = embedder.embed_query("The man chased the dog")
print(f"sim(e_1, e_2) = {cos_sim(e_1, e_2):.4f}")
print(f"sim(e_1, e_3) = {cos_sim(e_1, e_3):.4f}")
print(f"sim(e_2, e_3) = {cos_sim(e_2, e_3):.4f}")
print(f"sim(e_3, e_4) = {cos_sim(e_3, e_4):.4f}")
sim(e_1, e_2) = 0.5414
sim(e_1, e_3) = 0.5226
sim(e_2, e_3) = 0.7911
sim(e_3, e_4) = 0.8598
  • Note that sim(e_3, e_4) > sim(e_3, e_2) even though they seem to have the exact opposite meaning!
  • Why? There are many embeddings (e.g. bag of words) which make these close, and others where they are far apart. Hard to know without a sense of how it was trained.

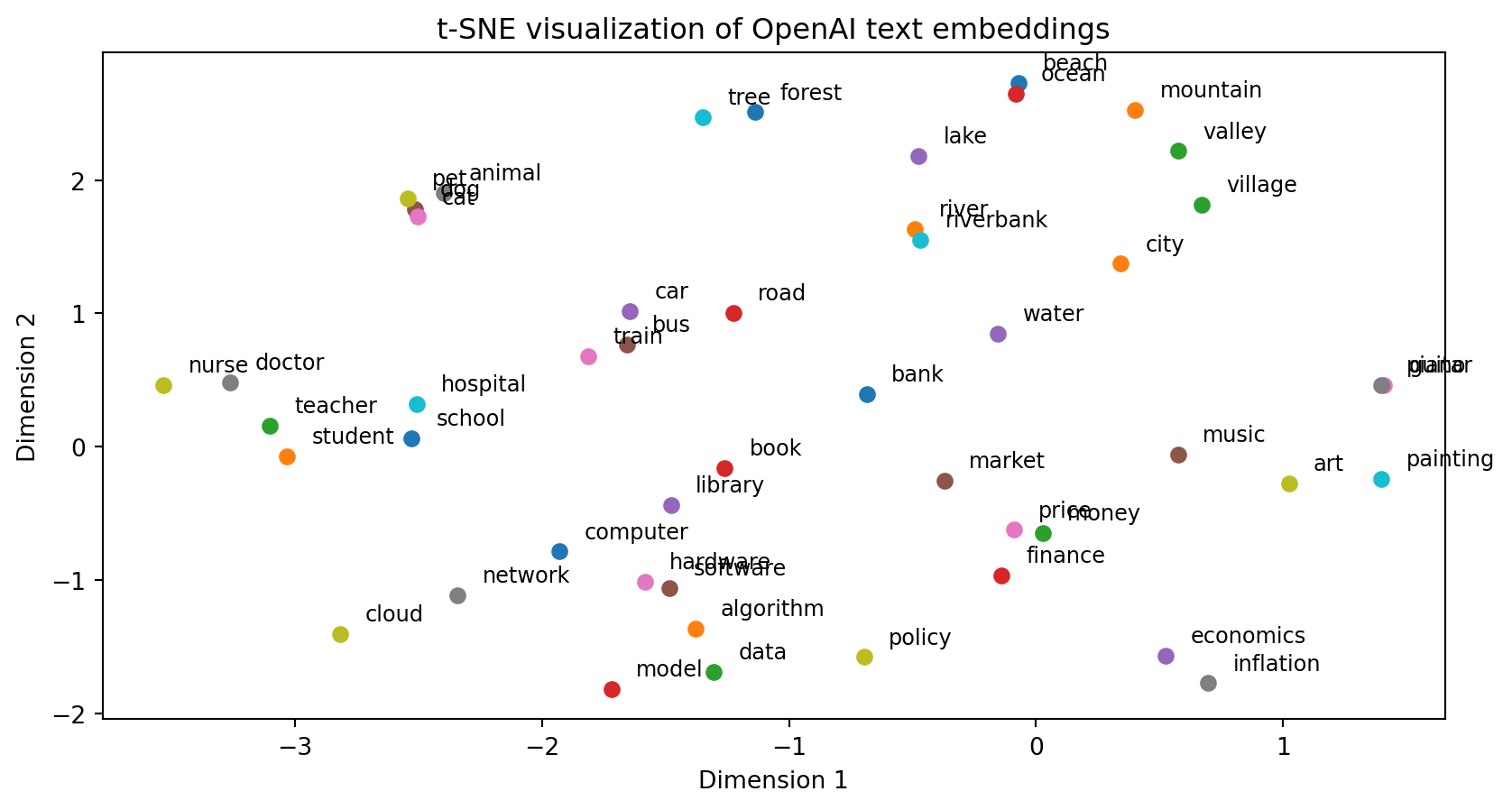
Clustering/Visualization

  • Since embeddings provide a measure of similarity/distance, we can cluster it into groups or use other tools to find interpretations
  • There are various algorithms to cluster based on representations, and find the closest elements within the set of data for a new element
  • One approach for visualization: come up with a lower-dimensional embedding which approximately preserves local neighborhoods in 2D/3D as in t-SNE (t-Distributed Stochastic Neighbor Embedding)

Get Some Random Embeddings

# Sample a small list of common words and embed them via OpenAIEmbeddings
sampled_tokens = [
  "bank", "river", "money", "finance", "water", "dog", "cat", "animal", "pet", "tree",
  "forest", "city", "village", "road", "car", "bus", "train", "doctor", "nurse", "hospital",
  "school", "student", "teacher", "book", "library", "music", "guitar", "piano", "art", "painting",
  "computer", "algorithm", "data", "model", "economics", "market", "price", "inflation", "policy",
  "riverbank", "beach", "mountain", "valley", "ocean", "lake", "software", "hardware", "network", "cloud"
]
embeddings = embedder.embed_documents(sampled_tokens)  # list[list[float]]
embeddings = np.array(embeddings)
print(f"collected {embeddings.shape[0]} embeddings of dimension {embeddings.shape[1]}")
collected 49 embeddings of dimension 3072

Visualize with t-SNE

tsne = TSNE(n_components=2, random_state=0)  # approx with 2D embedding
embeddings_2d = tsne.fit_transform(embeddings)
# Plot the t-SNE results
plt.figure()
for i, token in enumerate(sampled_tokens):
    x, y = embeddings_2d[i]
    plt.scatter(x, y)
    plt.text(x+0.1, y+0.1, token, fontsize=9)
plt.title('t-SNE visualization of OpenAI text embeddings')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()

Visualize with t-SNE

Sequential Data and Token Prediction

Distribution of Tokens

  • In many cases, data has an inherent sequential ordering. e.g. time series, language, etc.
  • Consider conditional probabilities over \(x_t \in \{1, \ldots K\}\). Generically call these “tokens”
  • Objects of interest: for \(x_1, x_2, \ldots, x_T\) for a sequence of length \(T\) sampled from some population distribution
  • We may want to condition on the past to predict the next token, condition on the entire sequence to predict missing ones, etc.

Multinomial Logit/Softmax

  • Often want to map a latent space to a probability distribution over \(K\) outcomes

  • Given a set of \(K\) outcomes, define the logit/softmax mapping a vector \(y \in \mathbb{R}^K\) to a probability distribution over \(K\) outcomes as \[ \mathrm{softmax}(y)_i = \frac{e^{y_i}}{\sum_{j=1}^K e^{y_j}}, \quad i = 1, \ldots, K \]

  • Typically this is combined with a mapping of a latent space, \(z \in \mathbb{R}^L\), with some matrix \(W \in \mathbb{R}^{K \times L}\) so that \(\mathrm{softmax}(W z)\) is a probability distribution over \(K\) outcomes

    \[ \mathbb{P}\left(x = k \,|\, z\right) = \mathrm{softmax}(W z)_k \]

Token Prediction from Conditional Probabilities

  • Given a sequence \(x_1, x_2, \ldots, x_{t-1}\), model the conditional distribution: \[ \mathbb{P}(x_t | x_{t-1}, x_{t-2}, \ldots, x_1) \]
    • Where in the background these are done with marginal and conditional probabilities sampling the population distribution
  • Basic strategy for sequence models:
    1. Do an embedding for each token \(\phi_1(x_t)\)
    2. Map those embeddings to some combined representation, \(\phi_2(\phi_1(x_1), \ldots, \phi_1(x_{t-1}))\)
    3. Map that with \(\mathrm{softmax}\) to get probabilities over \(k = 1, \ldots, K\) for \(x_t\)
    4. Fit with methods such as maximum likelihood given the multinomial logit structure

Provide Conditioning Tokens in the Prompt

resp = llm.invoke([
    SystemMessage(content="You provide 2 short bullet points, technical answers."),
    HumanMessage(content="What is an embedding?")
])
resp_text = resp.content
print(resp_text)

Provide Conditioning Tokens in the Prompt

- An embedding is a representation of discrete objects, such as words or items, in a continuous vector space, allowing for mathematical operations and capturing semantic relationships.
- It is commonly used in machine learning and natural language processing (NLP) to facilitate tasks like similarity measurement and clustering by translating high-dimensional data into lower-dimensional spaces.

Reminder: Concatenating Results

resp = llm.invoke([
    SystemMessage(content="You provide 2 short bullet points, technical answers."),
    HumanMessage(content="What is an embedding?"),
    AIMessage(content=resp_text),
    HumanMessage(content="What is the relationship to latent spaces?")
])
print(resp.content)

Reminder: Concatenating Results

- Embeddings can be considered a type of representation within a latent space, where the latent space captures the underlying structure and relationships of the data in a compressed format.
- Latent spaces are often learned through techniques like autoencoders or generative models, where embeddings serve as points in this space, reflecting the intrinsic properties of the original data.

Mental Model of Sequential Generation

  1. Start with a set of tokens, \(x_1, x_2, \ldots, x_{t-1}\) (include EVERYTHING)
  2. Condition on those tokens to find the \(\mathbb{P}(x_t | x_{t-1}, x_{t-2}, \ldots, x_1)\) distribution
  3. Sample from that to get the \(x_t\) token
    • “Temperature” setting mechanically increases/decreases the randomness for the logit (e.g., rescales \(W z\))
  4. Add its own generated token to the set of tokens, \(x_1, x_2, \ldots, x_{t-1}, x_t\)
  5. Condition on those tokens to find the \(\mathbb{P}(x_{t+1} | x_t, x_{t-1}, \ldots, x_1)\) distribution
  6. Repeat until it hits a special “done” token (itself predicted) or reaches a maximum length

Cardinality of the Estimated Conditional Distribution

  • ChatGPT and others generate text token-by-token auto-regressively
  • No directly Markov. \(K^T\) possible sequences of \(K\) tokens of length \(T\)
  • Modest sized LLMs in 2025 might support \(T=4,000\) with \(K=50,000\) tokens
    • Estimating a \(\mathbb{P} : 50,000 \times 50,000^{4,000}\to [0,1]\) conditional PMF
    • And growing. Many recent models have supports \(128k\) tokens for context (i.e., conditioning) and \(16k\) for “output”

How Can This Possibly Work?

  • It sometimes feels like it has compressed and memorized the entire internet
  • We don’t always know the parameterization or number of tokens in the training data (remember, this largely uses MLE to train) but OpenAI’s GPT-3 was disclosed
    • The \(\mathbb{P}(\cdot | \cdot)\) is approximated by approximating 175 billion parameters
    • Trained on 300 billion tokens from close to a terabyte of cleaned text
  • Which is an absurdly small amount of data given the cardinality of \(\mathbb{P}\)
    • Paraphrasing Mikhail Belkin: this is like estimating the Library of Congress with a molecule of ink.