Applications of Linear Algebra and Eigenvalues

Graduate Quantitative Economics and Datascience

Jesse Perla
jesse.perla@ubc.ca

University of British Columbia

Overview

Motivation and Materials

  • In this lecture, we will cover some applications of the tools we developed in the previous lecture
  • The goal is to build some useful tools to sharpen your intuition on linear algebra and eigenvalues/eigenvectors, and practice some basic coding

Extra Materials

Packages

import numpy as np
import matplotlib.pyplot as plt
import scipy
from numpy.linalg import cond, matrix_rank, norm
from scipy.linalg import inv, solve, det, eig, lu, eigvals
from scipy.linalg import solve_triangular, eigvalsh, cholesky

Difference Equations

Linear Difference Equations as Iterative Maps

  • Consider \(A : \mathbb{R}^N \to \mathbb{R}^N\) as the linear map for the state \(x_t \in \mathbb{R}^N\)
  • An example of a linear difference equation is \[ x_{t+1} = A x_t,\quad A \equiv \begin{bmatrix} 0.9 & 0.1 \\ 0.5 & 0.8 \\ \end{bmatrix} \]
A = np.array([[0.9, 0.1],
              [0.5, 0.8]])
x_0 = np.array([1, 1])
x_1 = A @ x_0
print(f"x_1 = {x_1}, x_2 = {A @ x_1}")
x_1 = [1.  1.3], x_2 = [1.03 1.54]

Iterating with \(\rho(A) > 1\)

Iterate \(x_{t+1} = A x_t\) from \(x_0\) for \(t=100\)

x_0 = np.array([1, 1])
t = 200
x_t = np.linalg.matrix_power(A, t) @ x_0
rho_A = np.max(np.abs(eigvals(A)))
print(f"rho(A) = {rho_A}")
print(f"x_{t} = {x_t}")
rho(A) = 1.079128784747792
x_200 = [3406689.32410673 6102361.18640516]
  • Diverges to \(x_{\infty} = \begin{bmatrix} \infty & \infty \end{bmatrix}^T\)
  • \(\rho = 1 + 0.079\) says in the worst case (i.e., \(x_t \propto\) the eigenvector associated with \(\lambda = 1.079\) eigenvalue), expands by \(7.9\%\) on each iteration

Iterating with \(\rho(A) < 1\)

A = np.array([[0.6, 0.1],
              [0.5, 0.8]])
x_t = np.linalg.matrix_power(A, t) @ x_0
rho_A = np.max(np.abs(eigvals(A)))
print(f"rho(A) = {rho_A}")
print(f"x_{t} = {x_t}")
rho(A) = 0.9449489742783178
x_200 = [6.03450418e-06 2.08159603e-05]
  • Converges to \(x_{\infty} = \begin{bmatrix} 0 & 0 \end{bmatrix}^T\)

Iterating with \(\rho(A) = 1\)

  • To make a matrix that has \(\rho(A) = 1\) reverse eigendecomposition!
  • Leave previous eigenvectors in \(Q\), change \(\Lambda\) to force \(\rho(A)\) directly
A = np.array([[0.9, 0.1],
              [0.5, 0.8]]) # rho(A) > 1
Lambda, Q = eig(A)
Lambda = [1.0, 0.8]
A = Q @ np.diag(Lambda) @ inv(Q)
x_t = np.linalg.matrix_power(A, t) @ x_0
print(f"Q =\n{Q}")
print(f"A =\n{A}")
print(f"rho(A) = {np.max(np.abs(eigvals(A)))}")
print(f"x_{t} = {x_t}")
print(f"||x_0|| = {norm(x_0)}")
print(f"||x_{t}|| = {norm(x_t)}")
Q =
[[ 0.48744474 -0.33726692]
 [ 0.87315384  0.94140906]]
A =
[[0.92182179 0.04364358]
 [0.21821789 0.87817821]]
rho(A) = 1.0
x_200 = [0.82732684 1.48198051]
||x_0|| = 1.4142135623730951
||x_200|| = 1.6972730813998493

Stretching?

  • Since \(\rho(A) = 1\) we have \(||x_t||\) cannot grow without bound, but \(\lambda_2 < 1\)
  • What if we are exactly on the eigenvector associated with \(\lambda_1 = 1\)?
# rescale eigenvector with lambda_1 = 1
x_0 = 4.2 * Q[:,0] 
x_t = np.linalg.matrix_power(A, t) @ x_0
print(f"x_0 = {x_0}")
print(f"x_{t} = {x_t}")
print(f"||x_0|| = {norm(x_0)}")
print(f"||x_{t}|| = {norm(x_t)}")
x_0 = [2.04726791 3.66724612]
x_200 = [2.04726791 3.66724612]
||x_0|| = 4.199999999999999
||x_200|| = 4.20000000000001

Disappearing?

  • What if we are exactly on the eigenvector associated with \(\lambda_2 = 0.8\)?
  • Not sure if there is a useful interpretation of the vector, though.
# rescale eigenvector with lambda_1 = 1
x_0 = 4.2 * Q[:,1] 
x_t = np.linalg.matrix_power(A, t) @ x_0
print(f"x_0 = {x_0}")
print(f"x_{t} = {x_t}")
print(f"||x_0|| = {norm(x_0)}")
print(f"||x_{t}|| = {norm(x_t)}")
x_0 = [-1.41652108  3.95391806]
x_200 = [5.53682082e-16 8.72332377e-16]
||x_0|| = 4.2
||x_200|| = 1.0332122842102235e-15

Unemployment Dynamics

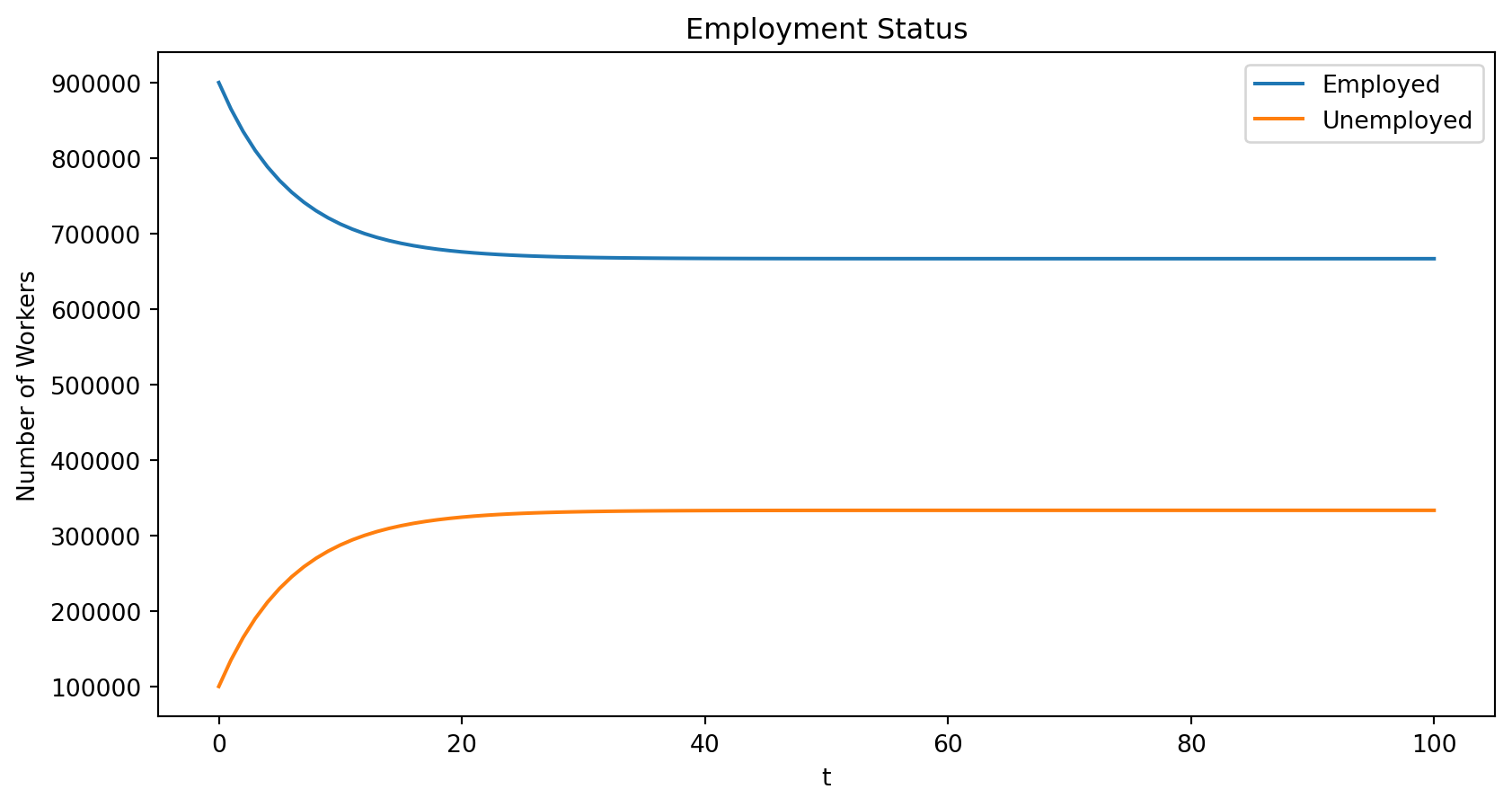
Dynamics of Employment without Population Growth

  • Consider an economy where in a given year \(\alpha = 5\%\) of employed workers lose job and \(\phi = 10\%\) of unemployed workers find a job
  • We start with \(E_0 = 900,000\) employed workers, \(U_0 = 100,000\) unemployed workers, and no birth or death. Dynamics for the year:

\[ \begin{aligned} E_{t+1} &= (1-\alpha) E_t + \phi U_t\\ U_{t+1} &= \alpha E_t + (1-\phi) U_t \end{aligned} \]

Write as Linear System

  • Use matrices and vectors to write as a linear system

\[ \underbrace{\begin{bmatrix} E_{t+1}\\U_{t+1}\end{bmatrix}}_{X_{t+1}} = \underbrace{\begin{bmatrix} 1-\alpha & \phi \\ \alpha & 1-\phi \end{bmatrix}}_{ A} \underbrace{\begin{bmatrix} E_{t}\\U_{t}\end{bmatrix}}_{X_t} \]

Simulating

Simulate by iterating \(X_{t+1} = A X_t\) from \(X_0\) until \(T=100\)

def simulate(A, X_0, T):
    X = np.zeros((2, T+1))
    X[:,0] = X_0
    for t in range(T):
        X[:,t+1] = A @ X[:,t]
    return X
X_0 = np.array([900000, 100000])
A = np.array([[0.95, 0.1], [0.05, 0.9]])
T = 100
X = simulate(A, X_0, T)
print(f"X_{T} = {X[:,T]}")
X_100 = [666666.6870779  333333.31292209]

Dynamics of Unemployment

fig, ax = plt.subplots()
ax.plot(range(T+1), X.T,
  label=["Employed", "Unemployed"])
ax.set(xlabel="t",
  ylabel="Number of Workers",
  title="Employment Status")
ax.legend()
plt.show()

Convergence to a Longrun Distribution

  • Find \(X_{\infty}\) by iterating \(X_{t+1} = A X_t\) many times from a \(X_0\)?

    • Check if it has converged with \(X_{\infty} \approx A X_{\infty}\)
    • Is \(X_{\infty}\) the same from any \(X_0\)? Will discuss “ergodicity” later

  • Alternatively, note that this expression is the same as

    \[ 1 \times \bar{X} = A \bar{X} \]

    • i.e, a \(\lambda = 1\) where \(\bar{X}\) is the corresponding eigenvector of \(A\)
    • Is \(\lambda = 1\) always an eigenvalue? (yes if all \(\sum_{n=1}^N A_{ni} = 1\) for all \(i\))
    • Does \(\bar{X} = X_{\infty}\)? For any \(X_0\)?
    • Multiple eigenvalues with \(\lambda = 1 \implies\) multiple \(\bar{X}\)

Using the First Eigenvector for the Steady State

Lambda, Q = eig(A)
print(f"real eigenvalues = {np.real(Lambda)}")
print(f"eigenvectors in columns of =\n{Q}")
print(f"first eigenvalue = 1? \
{np.isclose(Lambda[0], 1.0)}")
X_bar = Q[:,0] / np.sum(Q[:,0]) * np.sum(X_0)
print(f"X_bar = {X_bar}\nX_{T} = {X[:,T]}")
real eigenvalues = [1.   0.85]
eigenvectors in columns of =
[[ 0.89442719 -0.70710678]
 [ 0.4472136   0.70710678]]
first eigenvalue = 1? True
X_bar = [666666.66666667 333333.33333333]
X_100 = [666666.6870779  333333.31292209]

Using the Second Eigenvalue for the Convergence Speed

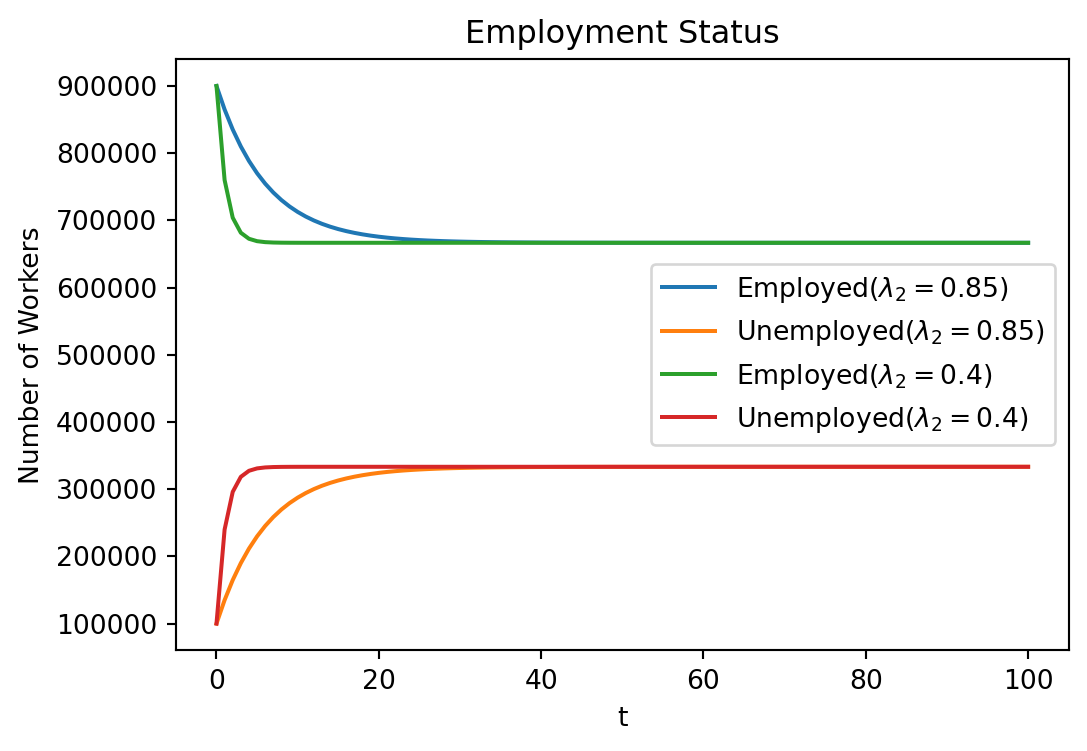
  • The second largest (\(\lambda_2 < 1\)) provides information on the speed of convergence
    • \(0\) is instantaneous convergence here
    • \(1\) is no convergence here
  • We will create a new matrix with the same steady state, different speed
    • To do this, build a new matrix with the same eigenvectors (in particular the same eigenvector associated with the \(\lambda=1\) eigenvalue)
    • But we will replace the eigenvalues \(\begin{bmatrix}1.0 & 0.85\end{bmatrix}\) with \(\begin{bmatrix}1.0 & 0.5\end{bmatrix}\)
    • Then we will reconstruct \(A\) matrix and simulate again
  • Intuitively we will see the that the resulting \(A_{\text{fast}}\) implies \(\alpha\) and \(\phi\) which are larger by the same proportion

Simulating with Different Eigenvalues

Lambda_fast = np.array([1.0, 0.4])
A_fast = Q @ np.diag(Lambda_fast) @ inv(Q) # same eigenvectors
print("A_fast =\n", A_fast)
print(f"alpha_fast/alpha = {A_fast[1,0]/A[1,0]:.2g}, \
phi_fast/phi = {A_fast[0,1]/A[0,1]:.2g}")
X_fast = simulate(A_fast, X_0, T)
print(f"X_{T} = {X_fast[:,T]}")
A_fast =
 [[0.8 0.4]
 [0.2 0.6]]
alpha_fast/alpha = 4, phi_fast/phi = 4
X_100 = [666666.66666667 333333.33333333]

Convergence Dynamics of Unemployment

Present Discounted Values

Basic Asset Pricing

  • Deterministic, infinite horizon, risk-neutral asset pricing based on fundamentals
  • Present-value of cashflows, dividends, etc.
  • Discount factor \(\beta \in (0,1)\)
    • Might come from consumer impatient, or an internal rate of return
    • Or can get out of risk-free interest rate \(r\) as \(\beta = \frac{1}{1+r}\) in some cases
  • Could price based on fundamentals as: \[ p_t = \sum_{s=0}^{\infty} \beta^s y_{t+s} \]

Scalar Aggregate State

  • Assume dividends follow \(y_{t+1} = a y_t\) for \(t=0,1,\ldots\) and \(y_0\) is given
  • \(a > 0\) shows how period-payoffs evolve. Can only be a growth or shrinkage factor here. \[ p_t = \sum_{s=0}^{\infty} \beta^s y_{t+s} = \frac{y_t}{1-\beta a} \]
    • Note that \(\beta a < 1\) is required for convergence
    • If \(a\) makes dividends grow faster than the discount rate, then the fundamental price is undefined
    • Of course, assets don’t grow forever, but if they grow for a long time this could still be a problem

Geometric Series for LSS

  • More generally for vector \(x_t\in\mathbb{R}^N\) capturing the relevant state of the world for payoff \(y_t\):
    • \(x_{t+1} = A x_t\) with \(y_t = G x_t\)
    • \(A \in \mathbb{R}^{N \times N}\) and \(G \in \mathbb{R}^{1 \times N}\) then
    • Called a linear state space model
    \[ \begin{aligned} p_t &= y_t + \beta y_{t+1} + \beta^2 y_{t+2} + \ldots = G x_t + \beta G A x_t + \beta^2 G A A x_t + \ldots\\ &= \sum_{s=0}^{\infty} \beta^s G A^s x_t\\ &= G (I - \beta A)^{-1} x_t\quad,\text{ if } \rho(A) < 1/\beta \end{aligned} \]

Convergence

  • \(G (I - \beta A)^{-1} x_t\) only has a solution if \(I - \beta A\) is invertible and yields positive \(p_t\)
  • Key condition: need spectral radius \(\rho(A) < 1/\beta\)
    • Intuition: the spectral radius is the maximum scaling of a vector in the worst possible direction.
    • This maximum expansion needs to be less than discounting of the infinite PDV is not defined
  • Special case of the scalar case with \(a > 0\)
  • \(A = \begin{bmatrix} a \end{bmatrix}\), \(G = \begin{bmatrix} 1 \end{bmatrix}\) and \(\rho(A) = a\)

PDV Example

Here is an example with \(1 < \rho(A) < 1/\beta\). Try with different \(A\)

beta = 0.9
A = np.array([[0.85, 0.1],
              [0.2, 0.9]])
G = np.array([[1.0, 1.0]]) # row vector
x_0 = np.array([1.0, 1.0])
p_t = G @ solve(np.eye(2) - beta * A, x_0)
#p_t = G @ inv(np.eye(2) - beta * A) @ x_0 # alternative
rho_A = np.max(np.abs(np.real(eigvals(A))))
print(f"p_t = {p_t[0]:.4g}, spectral radius = {rho_A:.4g}, 1/beta = {1/beta:.4g}")
p_t = 24.43, spectral radius = 1.019, 1/beta = 1.111